Acoustics Theory – Sound Behaviour in Closed Space

To understand sound behaviour in closed space better, we have to get into a bit of theory.

Room Acoustics

In this article, we will cover the physical nature of sound and its behaviour in closed space. Phenomena like resonance, interference, standing waves and similar will be explained. For easier understanding, basics of physics related to our topic will be discussed. The basic theory is indispensable when it comes to praxis. We will not do without understanding concepts like “wavelength” or “half wave”.

What Is Sound?

Sound is mechanical vibration formed by waves, occurring in matter, capable of inducing auditory perception. The frequencies that humans are capable to intercept—although quite individual—lie in the interval from 20 Hz to 20 000 Hz. Frequencies under 20 Hz, which can be heard by elephants, to give an example, are called infrasound. Frequencies higher than 20 kHz are called ultrasound. Dogs, dolphins, or bats are capable of intercepting them. Children in their younger years hear higher frequencies than adults. With advancing age, the hearable range decreases. Phenomena connected with origin of sound, its transmission and perception all fall under acoustics.

Image: Ultrasound_range_diagram.png: The original uploader was LightYear at English Wikipedia. Derivative work: Coolth CC BY-SA 3.0, via Wikimedia Commons

Speed of Sound / Frequency

The speed with which sound spreads is dependent on the conditions in the environment, primarily on temperature, pressure and humidity. At home, with 22°C, the speed of sound is approximately 345 m/s. Frequency is a physical quantity, which indicates repetition of a periodical phenomenon after a given period of time has elapsed. f=1/T, where f is frequency in Hertz (Hz) and T is the time period in seconds (s). If the distance between two walls of a listening space is 3.45 m, sound in air will overcome this distance in one hundredth of a second—1/100 s (0.01 s). Wavelength of this frequency is 100 Hz. Just to demonstrate: the hearable frequency range of 20 Hz to 20 kHz would translate into wavelengths ranging from 17.25 m to 1.7 cm.

Image: Indrajit Das CC BY-SA 3.0, via Wikimedia Commons

Reverberation

Duration of reverberation is absolutely fundamental when it comes to listening quality. It is the main parameter of room acoustics. The duration of reverberation is a time after which the volume of a sound impulse drops by 60 dB. In essence, it is the time after which acoustic energy disappears from the listening space. The duration of reverberation should fall somewhere between 0.25 and 0.5 s. The duration of reverberation is significantly influenced by acoustic materials present in a given space. Matching acoustic materials properly, using the right kind, amount and placement can to a great amount change the overall frequency characteristic of a room.

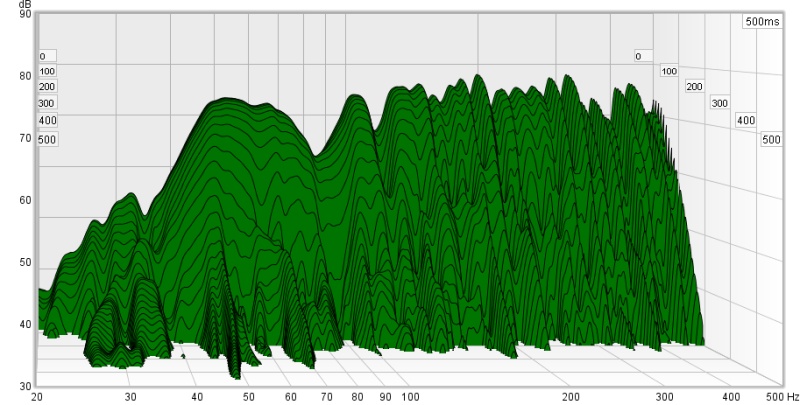
Frequency Characteristic of Reverberation

is determined by the duration of reverberation in relation to frequency. Each frequency in a given space has a different duration of reverberation. According to this characteristic, which is measurable, we can optimize the duration of reverberation on certain frequencies. While measuring, the microphone is placed where the ears of a listener would be. When measuring, notice that the frequency characteristic changes with different positioning of the speakers as well as of the listening place. These changes are accountable to the way sound behaves in closed space and to such phenomena as interference, resonance, etc.—as described further on.

Decibel dB

Decibel is a dimensionless unit, mostly used to measure the intensity level of sound. It is used in many other fields as well. Although it is, similarly to percentage, dimensionless, unlike percentage, decibel is a logarithmic unit. The definition of decibel is related to the discovery of the Weber-Fechner law. That is the human body perceives impulses logarithmically in relation to their intensity. The definition of decibel, formed in 1923 by the engineers of Bell’s laboratories was originally used to measure attenuation of telephone lines. For example a decrease (or attenuation) of 3 dB signifies 1/2 of power. On the other hand, an increase of 3 dB means double the power. Therefore, to increase acoustic pressure by sole 3 dB, we will need a twice as powerful amplifier.

dB Power Ratio and Amplitude Ratio

dB	Power Ratio		Amplitude Ratio
100	10 000 000 000		100 000
90	1 000 000 000		31 623
80	100 000 000		10 000
70	10 000 000		3 162
60	1 000 000		1 000
50	100 000		316	.2
40	10 000		100
30	1 000		31	.62
20	100		10
10	10		3	.162
6	3	.981	1	.995 (~2)
3	1	.995 (~2)	1	.413
1	1	.259	1	.122
0	1		1
−1	0	.794	0	.891
−3	0	.501 (~1/2)	0	.708
−6	0	.251	0	.501 (~1/2)
−10	0	.1	0	.316 2
−20	0	.01	0	.1
−30	0	.001	0	.031 62
−40	0	.000 1	0	.01
−50	0	.000 01	0	.003 162
−60	0	.000 001	0	.001
−70	0	.000 000 1	0	.000 316 2
−80	0	.000 000 01	0	.000 1
−90	0	.000 000 001	0	.000 031 62
−100	0	.000 000 000 1	0	.000 01
An illustration of power ratios x, or amplitude ratios √x and their equivalent in dB (10 log10x).

SPL

(Sound Pressure Level) is the ratio between a measured level of acoustic pressure and the human ear sensitivity threshold. SPL=20*log(S/Sref), where S is the measured acoustic pressure and Sref is the sensitivity threshold of the human ear (reference threshold acoustic pressure), defined by the value of 0.00002 N/m2 (newton per square metre). The human ear sensitivity threshold is different for different frequencies (Fletcher-Munson curves).

Distance Ratio of Listening Space Walls

Sound in an open environment acts in a completely different way compared to a closed space. In the open, sound leaves its source and freely spreads to all directions. In a room on the other hand, it bounces off the walls, floor, ceiling and furniture. The acoustic pressure is then a combination of a direct sound wave and its reflections. In a closed space, modal resonances and interference arise. Therefore, measurements show different values of acoustic pressure at various places in a room.

When playing any low sinusoidal frequency—300 Hz for example—and moving around the room, you will most certainly notice differences in volume. Resonance areas of intensification and weakening of the signal are dependent on the dimensions of a given room.

Three most optimal ratios of listening room wall distance are mentioned in literature. 1.00 is the floor to ceiling distance.

Ideal Ratios of Distances in the Listening Space

1.00 : 1.14 : 1.39
1.00 : 1.28 : 1.54
1.00 : 1.60 : 2.33

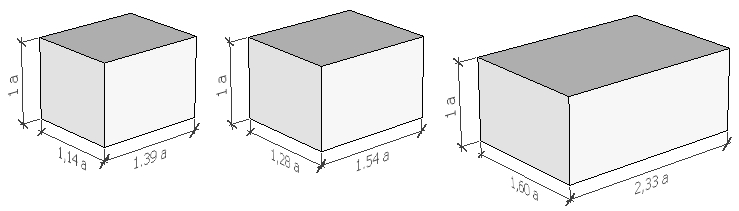
These ratios of opposite walls minimise formation of unwanted resonances. If you do not have a room with ideal wall distance ratios, do not despair, nothing is lost. With the help of properly placed bass traps, diffusers, resonators, or absorbers, a fairly acoustically balanced room is an achievable goal.

Modal Frequencies

These are integral multiples of the basic resonance frequency Fr. The wavelength is divided by two, which gives us a half wave, or the basic resonance frequency. Its multiples act the same way. If the resonance frequency is 50 Hz, integral multiples of that frequency will be the other resonance frequencies, also called modal frequencies. In our case it will be 50, 100, 150, 200, 250, 300, 350 Hz, …

Resonance

A listening space usually has the shape of a cuboid. Distances between the opposite walls determine a resonance frequency of this space. The resonance frequency can be calculated using the equation Fr=345/2L, where 345 m/s is the speed of sound in a common environment, 2 signifies a half wave and L is distance in metres. Fr is therefore the basic resonance frequency plus its harmonic components (integral multiples of this frequency). We live in a three-dimensional world, which means that we must calculate the resonances for front–back wall, side walls and ceiling–floor distances. With a 3.45 m wall distance, Fr will be 50 Hz (for a half wave), 100 Hz for a whole wave, plus its harmonic components (multiples) 3Fr (150Hz), 4Fr (200Hz), 5Fr (250Hz), …

Standing Waves

Standing waves develop when two waves with the same frequency going against each other meet. Usually, one of the waves is a direct wave, the other one a wave reflected from an obstacle. The reflected wave has a smaller amplitude than the original direct wave (because of energy losses during reflection). Places with minimal and maximal amplitude are formed as amplitudes of the resulting standing waves. Their ratio is called Standing Wave Ratio (SWR).

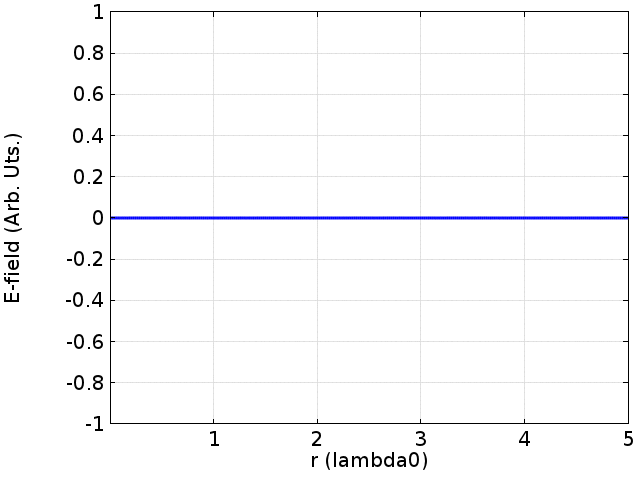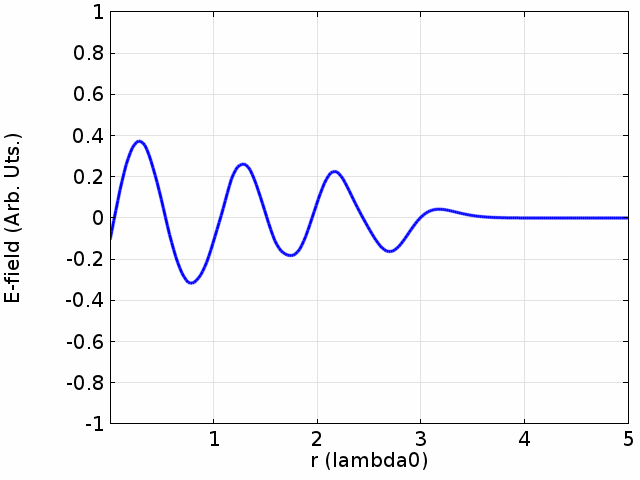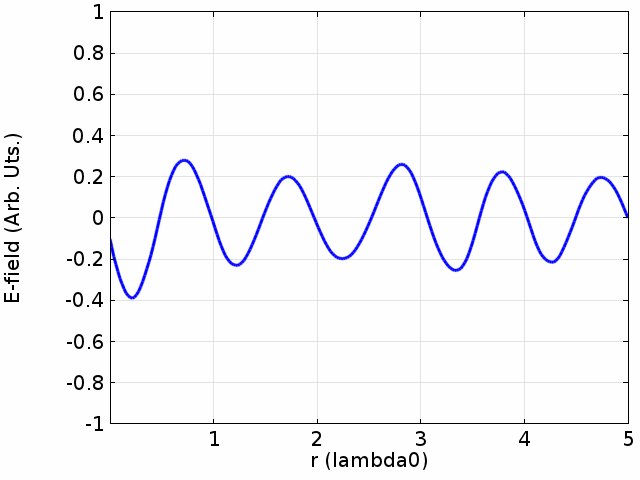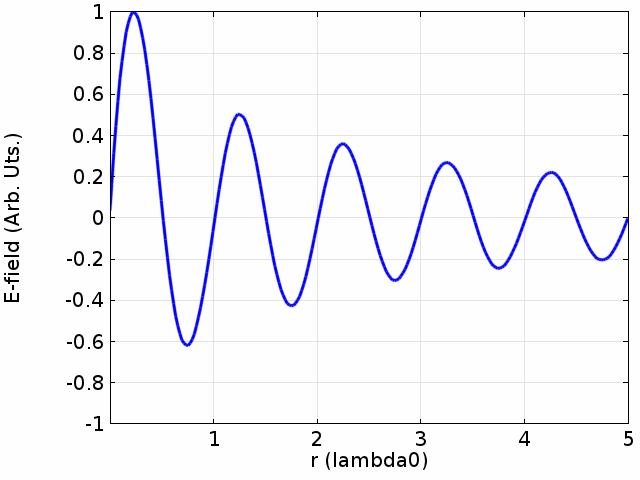
Image: Davidjessop CC BY-SA 4.0, via Wikimedia Commons

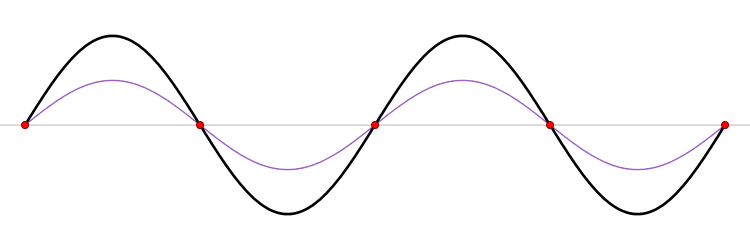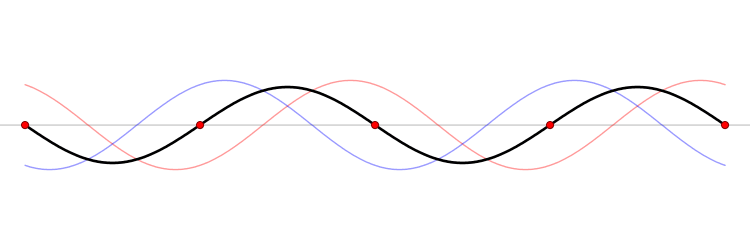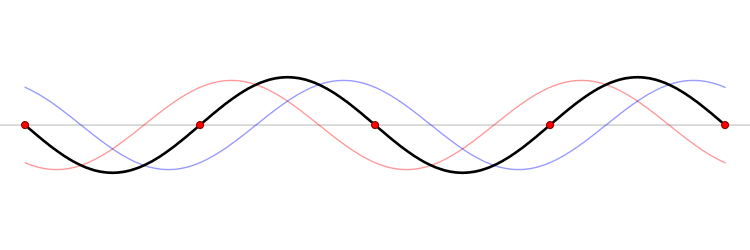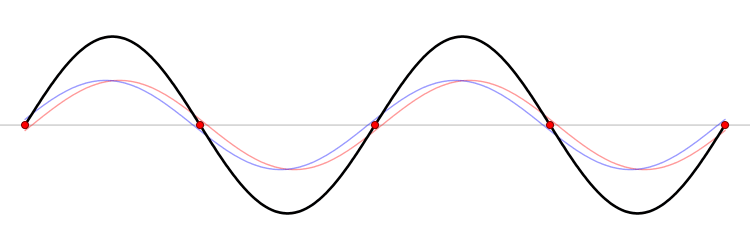
Interference

The interference phenomenon stands for acoustic waves affecting and intersecting each other. This is a characteristic behaviour of waves. During their movement and mingling, they are amplified at certain points and cancel each other out (or are attenuated) at others. These phenomena are illustrated using an interference pattern, where the alternating amplifications and weakenings are visible. When a number of waves coming from different sources spread through the environment, each of the waves spreads as if other waves would not exist in the environment. This characteristic property of waves is called the principle of the independence of wave transfer.

Wave Superposition

Thanks to the independent spreading of waves, they add up at places where they meet. The principles of addition of waves are similar to addition of vibrations. The result of wave addition is composite waves. Phenomena related to wave addition are called interference phenomena. Therefore we talk about interference of waves.

The resultant oscillating movement in a certain place is determined by the principle of superposition of individual waves. As a result of wave interference, amplitudes intensify and weaken at different places.

>Image: And1mu CC BY-SA 4.0, from Wikimedia Commons, unchanged

An alternative animation is available here.

Constructive Interference

occurs when two waves of the same phase meet. Constructive interference is basically an addition (summation) of wave amplitudes. It can arise in both positive and negative phases of a wave. 1+1=2 applies for the positive phase, (-1)+(-1)=-2 for the negative phase, the signal amplitude being 1 or (-1), respectively.

Destructive Interference

occurs when two waves with an opposite phase meet. Let us assume two waves approaching each other, one with an amplitude of +1 and the other of -1. At the moment when these waves completely overlap each other, the resulting value is 0. That means that both waves cancel each other completely and the acoustic pressure is zero.

Both constructive and destructive interference are not permanent. It is only a temporary phenomenon where one strength balances or multiplies the other one during their mutual clash. Addition of waves is based on the principle of superposition.

Image: original version: Haade; vectorization: Wjh31, Quibik CC BY-SA 3.0, via Wikimedia Commons

An animation is available here.

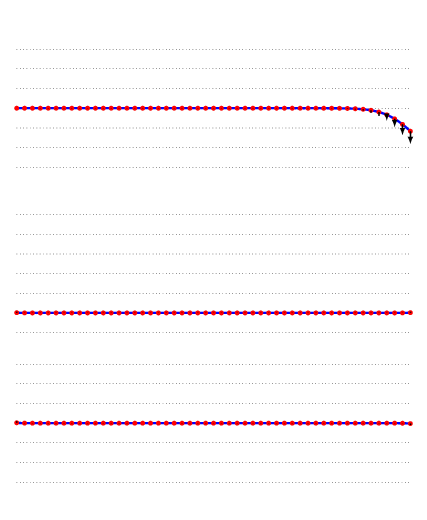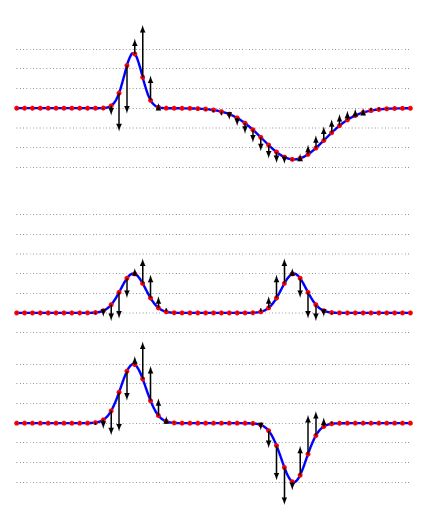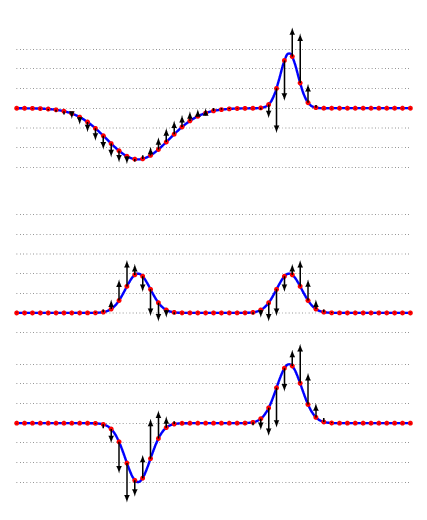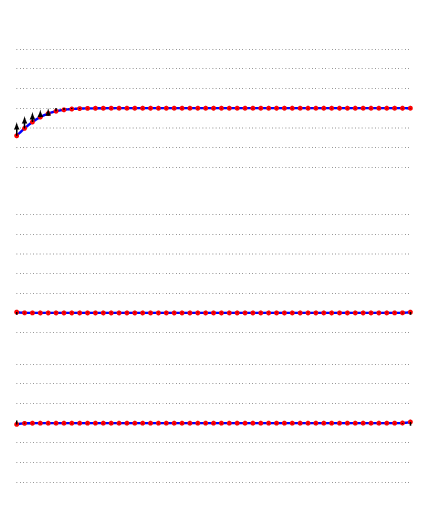
Beats

To complete the image of the complexity of issues related to space acoustics, another phenomenon accountable to interference has to be mentioned. Beats is a periodical and repeated fluctuation of sound volume occurring when two very similar frequencies influence each other. In other word, they are rhythms of interference. When two sound waves of similar frequency approach our ear, the changing constructive and destructive interference causes the sound to alternate between weaker and stronger intensity. In practice, we hear rhythmic differences in volume thanks to the difference in frequency of two waves sounding at the same time. A beats frequency is equal to the absolute value of a difference of two sound waves.

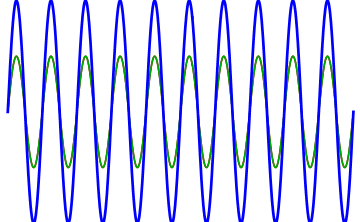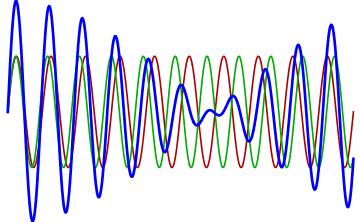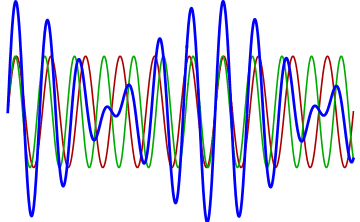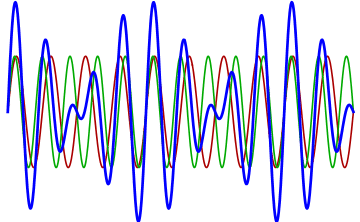
Image: Adjwilley CC BY-SA 3.0, from Wikimedia Commons

An alternative animation is available here.

Can be tested in practice (best with headphones). (When listening to only the right or the left channel, the phenomena disappears.)

Calculation and Simulation of Acoustics

Even though computing power is not such a problem these days, real simulation of the listening space with all its furnishings is pretty much impossible. The computational model would have to have all the information, precisely parameterized. Every acoustic material has its attenuation characteristic, which is dependent on frequency. They act differently with low, medium and high frequencies. With materials that are not perfectly flat, diffusion factor applies. Larger planes (a window, door, closet), show vibrations (flexibility/strength), etc.

The field of acoustics is comprehensive and complex. If we wanted a precise mathematical model of our room, it would always have to be based on measurements of reverberation taken at numerous points of the listening space. With the measurements prepared, a model would have to be constructed that acted in an absolutely identical way to the measured frequency characteristic and reverberation values at all the points. If anybody says that they are capable of achieving that, they most certainly lie. With some degree of inaccuracy, we can simulate only “something”—see the phenomena mentioned above.

In practice, real measurements of the duration of reverberation are used. Based on them, estimated appropriate acoustic adjustments are proposed.

We have become acquainted with the basic phenomena that apply in a closed space. How to divide the sound frequency characteristic, find weak spots and their solution is discussed in another article: Room Acoustics: not just for Audiophiles.

Links

https://www.acs.psu.edu/drussell/demos/superposition/superposition.html